Phase Information

Phase Elimination

When using the Fast Fourier Transform to boost the periodic characteristics of a signal, it is possible to eliminate phase information if phase is not important. Neural Lab provides the spectrum function to compute the FFT by eliminating phase information. The spectrum function returns the magnitude of the FFT (the squared root of the squared real part plus the squared imaginary part).

Phase Normalization

In some cases, the phase can be normalized using the phase of the highest frequency component. Neural Lab provides the functions: fftnorm and realfftnorm to compute the FFT by normalizing the phase. In a normalized phase signal, the phase of the harmonics is normalized using as reference the main harmonic.

Tip

Phase information elimination or phase normalization can enormously simplify the information applied to an ANN.

Noisy Periodic Signal

When the Fourier Transform of a noisy periodic signal is computed, each periodic component of the signal will be concentrated, while the noise component will be dispersed. Thus, the Fourier Transform of a noisy signal may provide a clearer view of the signal than the original signal.

Problem 1

Create a New Project called WithoutPhase (You must select: Multi-layer Network and Classification in the New Project Dialog) to test phase normalization. Add a file called BuildDataSet.lab to build an appropriate training set for the classification of the two shapes use 800 training cases for ANN with 128 inputs.

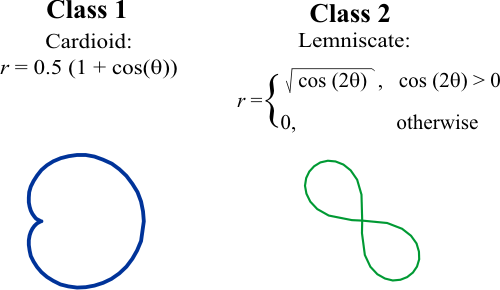
WithoutPhase\BuildDataSet.lab

int numCases = 800/2;
int numInputs = 128;
double deltaInput = 6.2832/numInputs;
int i;
int j;
double phase = 0.0;
//________________________________ Class 1: Cardioid
Matrix inputCardioid;
inputCardioid.Create(numCases, numInputs);
Matrix targetCardioid;
targetCardioid.Create(numCases, 2);

for(i=0; i<numCases; i++)
{
     phase = rand(6.2832);
     for (j=0; j<numInputs; j++)
     {
          inputCardioid[i][j] = 0.5*(1.0 + cos(phase + j*deltaInput));
     }
     targetCardioid[i][0] = 1;
}
//________________________________ Class 2: Lemniscate
Matrix inputLemniscate;
inputLemniscate.Create(numCases, numInputs);
Matrix targetLemniscate;
targetLemniscate.Create(numCases, 2);
double tmp;
for(i=0; i<numCases; i++)
{
     phase = rand(6.2832);
     for (j=0; j<numInputs; j++)
     {
          tmp = cos(phase + 2.0*j*deltaInput);
          if (tmp > 0.0)
          {
               inputLemniscate[i][j] = sqrt(tmp);
          }
     }
     targetLemniscate[i][1] = 1;
}
//_______________________________ Create the data set input
Matrix dataSetInput;
dataSetInput.AppendDown(inputCardioid);
dataSetInput.AppendDown(inputLemniscate);
dataSetInput.Save();
//_______________________________ Create the data set target
Matrix trainSetTarget;
trainSetTarget.AppendDown(targetCardioid);
trainSetTarget.AppendDown(targetLemniscate);
trainSetTarget.Save();

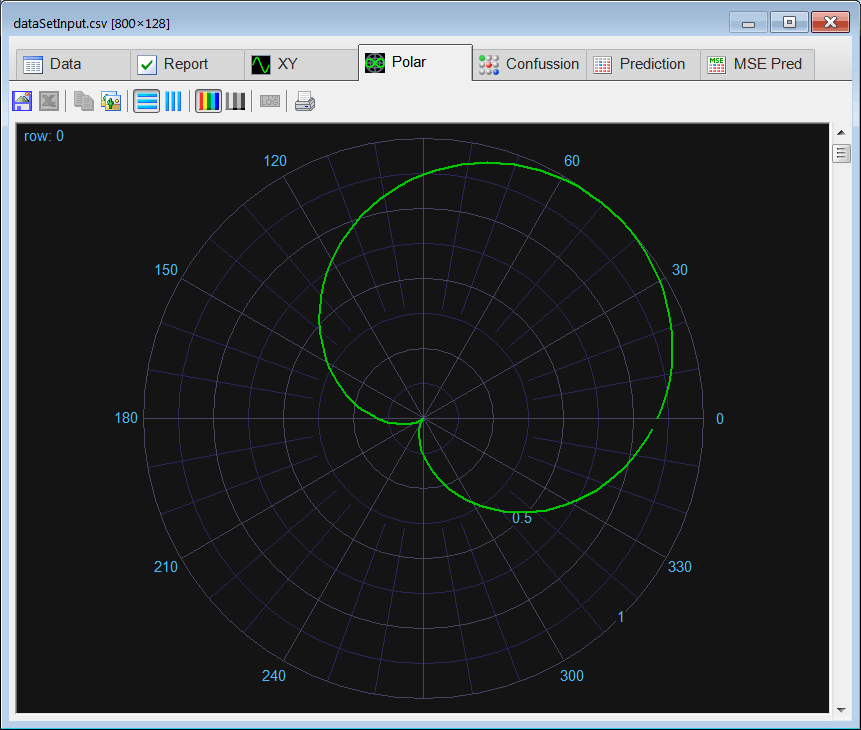
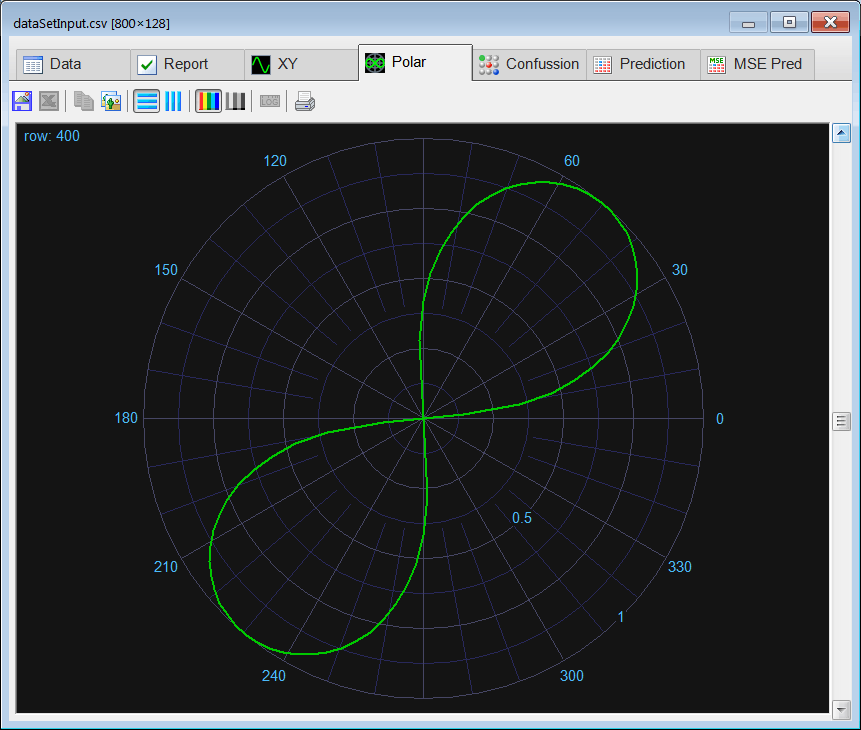
Problem 2

Edit the BuildTrainSet.lab file to create the training set using the Fast Fourier Transform by using the spectrum (or the realfftnorm) function. When the training set is ready, create and review the report by column for the training set input.

WithoutPhase\BuildTrainSet.lab

Matrix dataSetInput;
dataSetInput.Load();

Matrix trainSetInput = spectrum(dataSetInput);
//Matrix trainSetInput = realfftnorm(dataSetInput);
trainSetInput.Save();

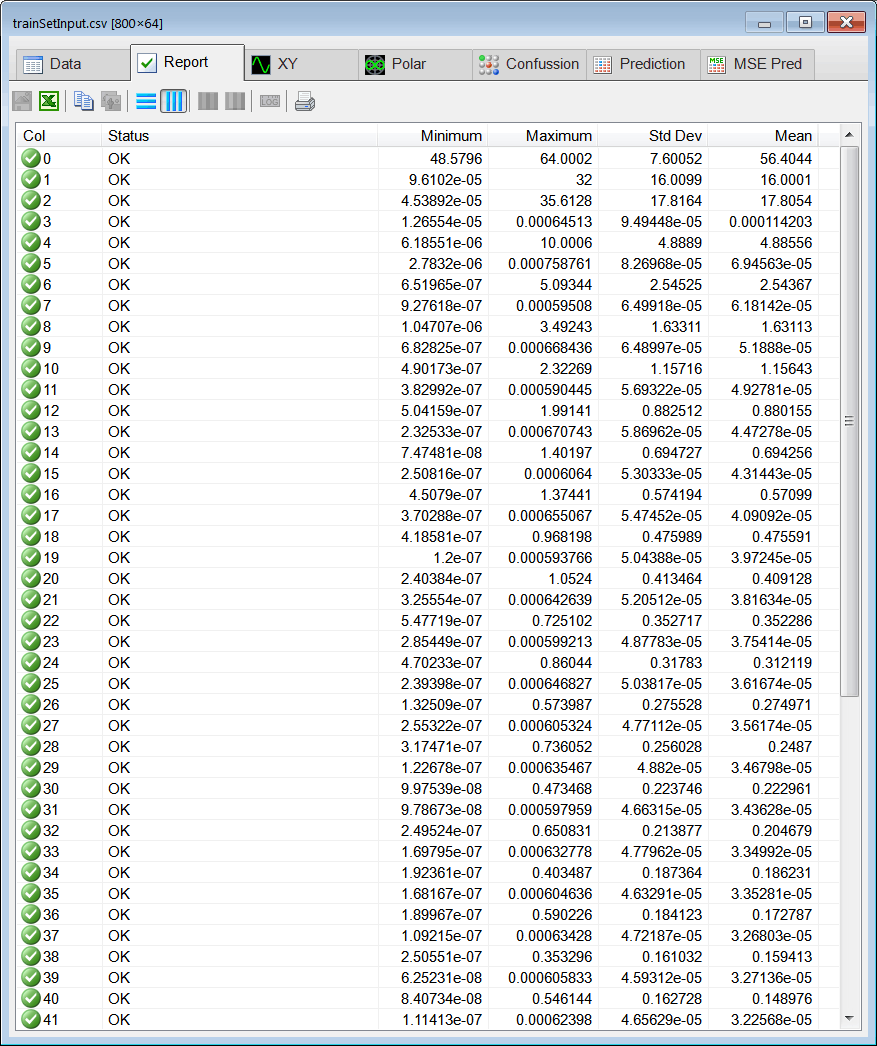
Problem 3

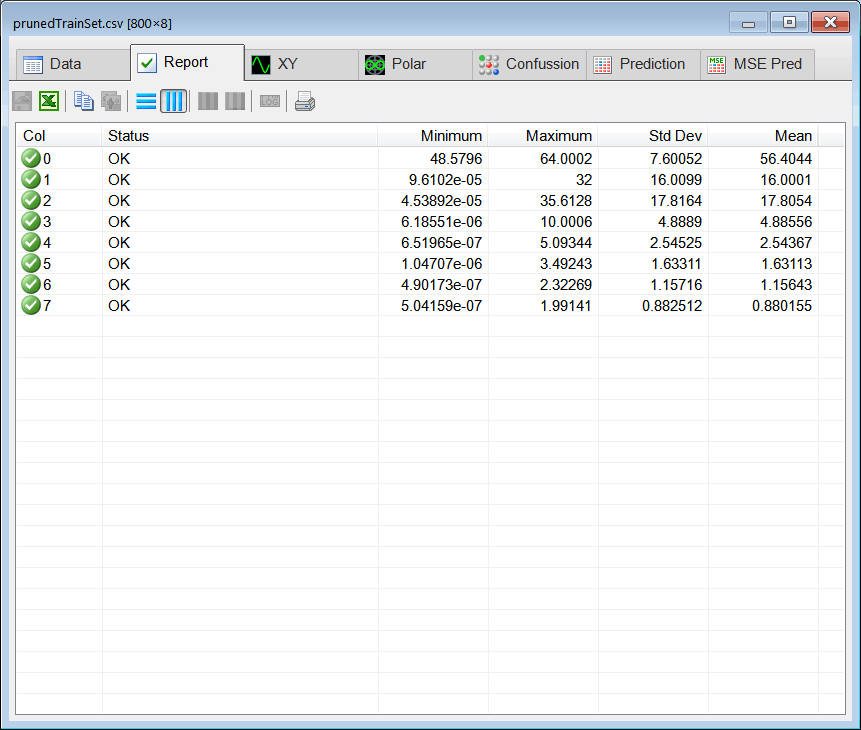
As it can be seen many columns in the training set input have little information. Prune the training set by removing those columns that have a variance that is less than 0.5.

WithoutPhase\Prune.lab

Matrix trainSetInput;
trainSetInput.Load();
int numRows = trainSetInput.GetRowCount();
//______________________________ Compute the Variance
Vector varianceInput = trainSetInput.ColsVar();

//______________________________ Compute how many columns we keep
int numCols = varianceInput.GetSize();
int count = 0;
int i;
for(i = 0; i < numCols; i++)
{
     if (varianceInput[i] > 0.5) count++;
}

//____________________________ Find which columns we keep
Vector keep;
keep.Create(count);
int j = 0;
for(i = 0; i < numCols; i++)
{
     if (varianceInput[i] > 0.5)
     {
          keep[j] = i;
          j++;
     }
}
keep.Save();
//_____________________________ Create the Pruned Train Set
Matrix prunedTrainSet;
prunedTrainSet = trainSetInput.GetCols(keep);
prunedTrainSet.Save();

Problem 4

Edit the BuilValidSet.lab file to build an appropriate validation set using 60 % of noise.

WithoutPhase\BuildValidSet.lab

Matrix dataSetInput;
dataSetInput.Load();

Vector keep;
keep.Load();

int rows = dataSetInput.GetRowCount();
int cols = dataSetInput.GetColCount();
Matrix noise;
noise.CreateRandom(rows, cols, 0.0, 1.0);

Matrix contaminated = 0.4*dataSetInput+0.6*noise;
Matrix normalized = spectrum(contaminated);
//Matrix normalized = realfftnorm(contaminated);
Matrix validSetInput = normalized.GetCols(keep);
validSetInput.Save();

Problem 5

Edit the Train.lab file to design and train an ANN for the classification of the shapes.

WithoutPhase\Train.lab

//_________________________ Network Setup
LayerNet net;
net.Create(8, 2, 0, 2);

//________________________ Load the training set
Matrix prunedTrainSet;
prunedTrainSet.Load();
Matrix trainSetTarget;
trainSetTarget.Load();

int i = 0;
//____________________________ Input Scaling
for(i = 0; i<8; i++)
{
//net.SetInScaler(i, -6.0, 64.0);
net.SetInScaler(i, 0.0, 64.0);
}
//____________________________ Output Scaling
net.SetOutScaler(0, 0.0, 1.0); // Output values are from 0 to 1
net.SetOutScaler(1, 0.0, 1.0); // Output values are from 0 to 1

//________________________ Set the training set
net.SetTrainSet(prunedTrainSet, trainSetTarget, false);

//________________________ Train
net.TrainSimAnneal(100, 100, 15, 0.001, false, 4, 1.0e-20);
net.TrainConjGrad(1000,1.0e-20);

//_____________________________ Save the trained network
net.Save();

Problem 6

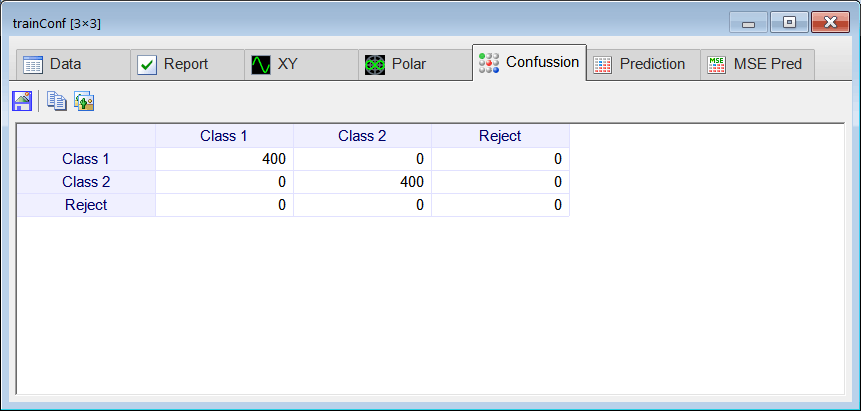
Edit the CheckTraining.lab file to check the training: (a) Compute the confusion matrix using the training set. (b) Plot the error for each network output. (c) Save the confusion matrix as a vector image (trainConf.emf).

WithoutPhase\CheckTraining.lab

//_________________________________________ Load the training set
Matrix prunedTrainSet;
prunedTrainSet.Load();
Matrix trainSetTarget;
trainSetTarget.Load();
//_________________________________________ Load the ANN
LayerNet net;
net.Load();
//_________________________________________ Run
Matrix output = net.Run(prunedTrainSet);
//_________________________________________ Compute the confusion matrix
Matrix trainConf = ConfusionMatrix(output, trainSetTarget, 0.5);
trainConf.Save();
//_________________________________________ Compute the Number of Errors
int numErrors = toint(trainConf.GetSum()) - toint(trainConf.GetDiagonalSum());

Problem 7

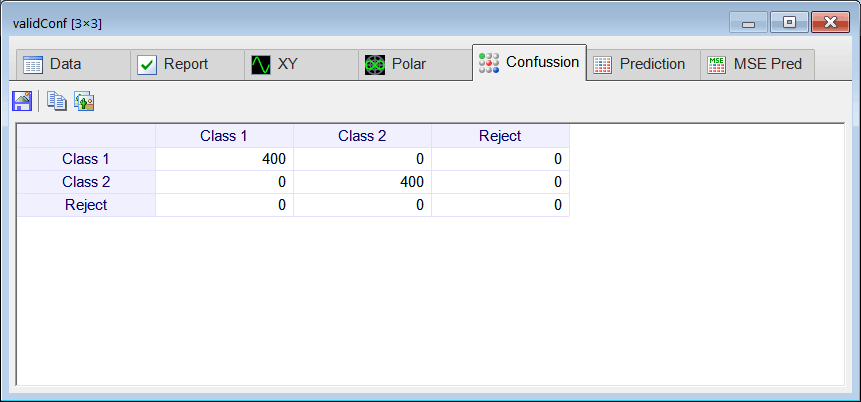
Edit the Validation.lab file to perform the validation of the ANN. (a) Compute the confusion matrix using the validation set. (b) Plot the error for each network output. (c) Save the confusion matrix as a vector image (validConf.emf).

Problem 8

Generate a report in Microsoft Word. Write some conclusions in the report trying to compare your results using data in the time domain with the data in the frequency domain. Discuss also the time it took to train when using data in the frequency domain.

Phase Information

Phase Elimination

Phase Normalization

Noisy Periodic Signal

© Copyright 2000-2021 Wintempla selo. All Rights Reserved. Jul 22 2021. Home